Is This a Binary Search Tree?| Tree
Task(medium)
For the purposes of this challenge, we define a binary tree to be a binary search tree with the following ordering requirements:
- The data value of every node in a node's left subtree is less than the data value of that node.
- The data value of every node in a node's right subtree is greater than the data value of that node.
Given the root node of a binary tree, can you determine if it's also a binary search tree?Complete the function in your editor below, which has 1 parameter: a pointer to the root of a binary tree. It must return a boolean denoting whether or not the binary tree is a binary search tree. You may have to write one or more helper functions to complete this challenge.
Input Format
You are not responsible for reading any input from stdin. Hidden code stubs will assemble a binary tree and pass its root node to your function as an argument.
Constraints
0 <= data <= 104
Output Format
You are not responsible for printing any output to stdout. Your function must return true if the tree is a binary search tree; otherwise, it must return false. Hidden code stubs will print this result as a Yes or No answer on a new line.
Sample Input
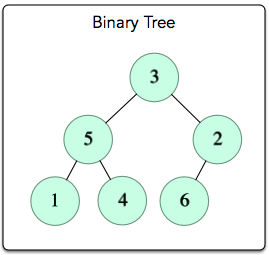
Sample Output
No
SOLUTION 1
def inorder(root, lst):
if root:
inorder(root.left, lst)
lst.append(root.data)
inorder(root.right, lst)
else:
return
def check_binary_search_tree_(root):
lst = []
inorder(root, lst)
prev = -1000
for x in lst:
print(x)
if prev >= x:
return "No"
prev = x
return "Yes"
EXPLANATION STEPS
-
In-Order Traversal Check: Perform an in-order traversal of the tree, which visits nodes in increasing order for a BST.As you traverse, check if the current node's value is greater than the previous node's value. If not, the tree is not a BST.
-
Recursive Range Check: Each node must lie within a specific range of values: For the root, the range is (−∞,∞)(-∞, ∞)(−∞,∞). For a left child, the value must be less than its parent's value. For a right child, the value must be greater than its parent's value. Recursively check that each node falls within its allowed range.

