Huffman Decoding| Tree
Task(medium)
Huffman coding assigns variable length codewords to fixed length input characters based on their frequencies. More frequent characters are assigned shorter codewords and less frequent characters are assigned longer codewords. All edges along the path to a character contain a code digit. If they are on the left side of the tree, they will be a 0 (zero). If on the right, they'll be a 1 (one). Only the leaves will contain a letter and its frequency count. All other nodes will contain a null instead of a character, and the count of the frequency of all of it and its descendant characters.
For instance, consider the string ABRACADABRA. There are a total of 11 characters in the string. This number should match the count in the ultimately determined root of the tree. Our frequencies are A=2,R=2,B=3,C=1 and D=1. The two smallest frequencies are for C and D, both equal to 1, so we'll create a tree with them. The root node will contain the sum of the counts of its descendants, in this case 1+1=2. The left node will be the first character encountered, C, and the right will contain D. Next we have 3 items with a character count of 2: the tree we just created, the character B and the character R. The tree came first, so it will go on the left of our new root node. B will go on the right. Repeat until the tree is complete, then fill in the 1's and 0's for the edges. The finished graph looks like:
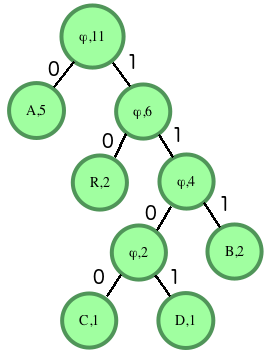
Input characters are only present in the leaves. Internal nodes have a character value of ϕ (NULL). We can determine that our values for characters are:
A - 0
B - 111
C - 1100
D - 1101
R - 10
Our Huffman encoded string is:
A B R A C A D A B R A
0 111 10 0 1100 0 1101 0 111 10 0
or
01111001100011010111100
To avoid ambiguity, Huffman encoding is a prefix free encoding technique. No codeword appears as a prefix of any other codeword.
To decode the encoded string, follow the zeros and ones to a leaf and return the character there.
You are given pointer to the root of the Huffman tree and a binary coded string to decode. You need to print the decoded string.
Function Description
Complete the function decode_huff in the editor below. It must return the decoded string.
decode_huff has the following parameters:
- root: a reference to the root node of the Huffman tree
- s: a Huffman encoded string
Input Format
There is one line of input containing the plain string s . Background code creates the Huffman tree then passes the head node and the encoded string to the function.
Constraints
1<= |S| <= 25.
Output Format
Output the decoded string on a single line.
Sample Input
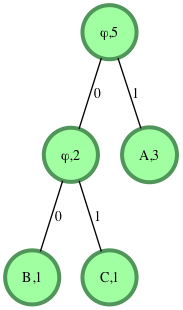
s="1001011"
Sample Output
ABACA
Explanation
S="1001011"
Processing the string from left to right.
S[0]='1' : we move to the right child of the root. We encounter a leaf node with value 'A'. We add 'A' to the decoded string.
We move back to the root.
S[1]='0' : we move to the left child.
S[2]='0' : we move to the left child. We encounter a leaf node with value 'B'. We add 'B' to the decoded string.
We move back to the root.
S[3] = '1' : we move to the right child of the root. We encounter a leaf node with value 'A'. We add 'A' to the decoded string. We move back to the root.
S[4]='0' : we move to the left child.
S[5]='1' : we move to the right child. We encounter a leaf node with value C'. We add 'C' to the decoded string.
We move back to the root.
S[6] = '1' : we move to the right child of the root. We encounter a leaf node with value 'A'. We add 'A' to the decoded string.
We move back to the root.
Decoded String = "ABACA"
SOLUTION 1
def decodeHuff(root, s):
head = root
for b in s:
if b == '0':
head = head.left
if head.data != chr(0):
print(head.data, end='')
head = root
else:
head = head.right
if head.data != chr(0):
print(head.data, end='')
head = root
EXPLANATION STEPS
-
Frequency Calculation:
- Calculate the frequency of each character in the given string.
-
Build a Min-Heap:
- Create a priority queue (min-heap) to store the characters along with their frequencies.
- Each node in the heap represents a character and its frequency.
-
Build the Huffman Tree:
- Extract two nodes with the lowest frequencies from the min-heap.
- Create a new internal node with these two nodes as children and with a frequency equal to the sum of the two nodes' frequencies.
- Insert the new node back into the min-heap.
- Repeat this process until only one node remains in the heap. This node becomes the root of the Huffman tree.
-
Generate Huffman Codes:
- Traverse the Huffman tree from the root to the leaves. Assign a '0' to the left edge and a '1' to the right edge.
- The code for each character is the path from the root to the corresponding leaf node.
- Store the codes for each character in a dictionary.
-
Encoding the Input String:
- Replace each character in the input string with its corresponding Huffman code to get the encoded string.
-
Decoding the Encoded String:
- Use the Huffman tree to decode the encoded string by traversing from the root based on the bits ('0' or '1') and extracting the characters.

