Kitty’s Calculation on a tree| Tree
Task(hard)
Kitty has a tree, T, consisting of n nodes where each node is uniquely labeled from 1 to n. Her friend Alex gave her q sets, where each set contains k distinct nodes. Kitty needs to calculate the following expression on each set:
where:
- denotes an unordered pair of nodes belonging to the set.
- denotes the number of edges on the unique (shortest) path between nodes u and v.
Example
The graph looks like this:
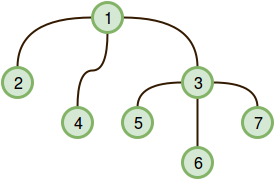
There are three pairs that can be created from the query set: . The distance from to is , from to is , and from to is .
Now do the summation:
Input Format
The first line contains two space-separated integers, the respective values of (the number of nodes in tree ) and (the number of nodes in the query set).
Each of the subsequent lines contains two space-separated integers, and , that describe an undirected edge between nodes and .
The subsequent lines define each set over two lines in the following format:
- The first line contains an integer, k, the size of the set.
- The second line contains k space-separated integers, the set's elements.
Constraints
1<=n<=2.105
1<=a,b<=n
1<=q<=105
1<=ki<=105
The sum of ki over all q does not exceed 2.105.
All elements in each set are distinct.
Subtasks
1<=n<=2000 for 24% of the maximum score.
1<=n<=5.104 for 45% of the maximum score.
1<=n<=2.105 for 100% of the maximum score.
Output Format
Print q lines of output where each line i contains the expression for the ith query, modulo 109+7.
Sample Input 0
7 3
1 2
1 3
1 4
3 5
3 6
3 7
2
2 4
1
5
3
2 4 5
Sample Output 0
16
0
106
SOLUTION 1
from collections import defaultdict
from itertools import combinations
n, q = [int(i) for i in input().split()]
edges = defaultdict(set)
for line in range(n-1):
a,b = [int(i) for i in input().split()]
edges[a].add(b)
edges[b].add(a)
def distance(beginning, end, dist):
if not options[beginning]:
return 0
if end in options[beginning]:
return dist + 1
next_ = options[beginning]
for n in next_:
options[n].discard(beginning)
return sum([distance(end, n, dist+1) for n in next_])
for set_def in range(q):
k = input()
query = {int(s) for s in input().split()}
if len(query) == 1:
print(0)
continue
comb = combinations(query,2)
options = edges.copy()
print(sum([a*b*(distance(a,b,0)) for a,b in comb])%(10**9 + 7))
EXPLANATION STEPS
1.Input Parsing: Read the number of nodes NNN and the number of queries QQQ. For each query, read the number of nodes in the subset and the nodes themselves.
2.Tree Representation: Use an adjacency list to represent the tree. For each edge, add the nodes to each other's list.
3.Precompute Distances Using BFS or DFS: Select a random node as the root (often node 1) and perform a Breadth-First Search (BFS) or Depth-First Search (DFS) to calculate the distance from the root to all other nodes. This is to precompute the depth of each node. Store the parent of each node and the depth from the root.
4.Lowest Common Ancestor (LCA) Precomputation: Precompute the LCA for each pair of nodes using a sparse table method or binary lifting. This helps in calculating the distance between any two nodes in O(logN)O(\log N)O(logN) time.
5.Distance Calculation: For each query, given the subset of nodes SSS, calculate the sum of distances between all pairs of nodes in S.
6.Result Calculation: For each query, iterate over all pairs of nodes in the subset and compute the sum of their distances using the precomputed depth and LCA information.

